Studying Hohmann transfers¶
[1]:
from astropy import units as u
from matplotlib import pyplot as plt
import numpy as np
from poliastro.bodies import Earth
from poliastro.maneuver import Maneuver
from poliastro.twobody import Orbit
from poliastro.util import norm
[2]:
Earth.k
[2]:
$3.9860044 \times 10^{14} \; \mathrm{\frac{m^{3}}{s^{2}}}$
[3]:
orb_i = Orbit.circular(Earth, alt=800 * u.km)
orb_i
[3]:
7178 x 7178 km x 0.0 deg (GCRS) orbit around Earth (♁) at epoch J2000.000 (TT)
[4]:
r_i = orb_i.a.to(u.km)
r_i
[4]:
$7178.1366 \; \mathrm{km}$
[5]:
v_i_vec = orb_i.v.to(u.km / u.s)
v_i = norm(v_i_vec)
v_i
[5]:
$7.4518315 \; \mathrm{\frac{km}{s}}$
[6]:
N = 1000
dv_a_vector = np.zeros(N) * u.km / u.s
dv_b_vector = dv_a_vector.copy()
r_f_vector = r_i * np.linspace(1, 100, num=N)
for ii, r_f in enumerate(r_f_vector):
man = Maneuver.hohmann(orb_i, r_f)
(_, dv_a), (_, dv_b) = man.impulses
dv_a_vector[ii] = norm(dv_a)
dv_b_vector[ii] = norm(dv_b)
/home/docs/checkouts/readthedocs.org/user_builds/poliastro/envs/latest/lib/python3.9/site-packages/poliastro/core/maneuver.py:49: NumbaPerformanceWarning: '@' is faster on contiguous arrays, called on (Array(float64, 1, 'A', False, aligned=True), Array(float64, 1, 'A', False, aligned=True))
r_i = norm(r_i)
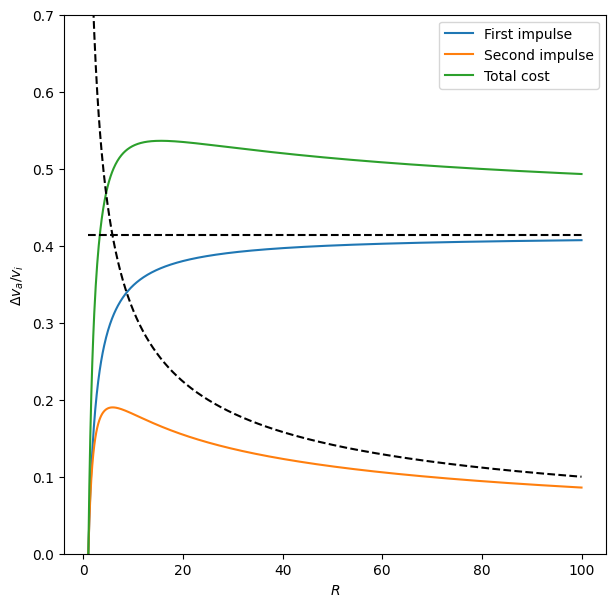
[7]:
fig, ax = plt.subplots(figsize=(7, 7))
ax.plot(
(r_f_vector / r_i).value, (dv_a_vector / v_i).value, label="First impulse"
)
ax.plot(
(r_f_vector / r_i).value, (dv_b_vector / v_i).value, label="Second impulse"
)
ax.plot(
(r_f_vector / r_i).value,
((dv_a_vector + dv_b_vector) / v_i).value,
label="Total cost",
)
ax.plot((r_f_vector / r_i).value, np.full(N, np.sqrt(2) - 1), "k--")
ax.plot((r_f_vector / r_i).value, (1 / np.sqrt(r_f_vector / r_i)).value, "k--")
ax.set_ylim(0, 0.7)
ax.set_xlabel("$R$")
ax.set_ylabel("$\Delta v_a / v_i$")
plt.legend()
fig.savefig("hohmann.png")